Uncertainty in Earthquake Ground Motion: Which NGA Equation Is Right?

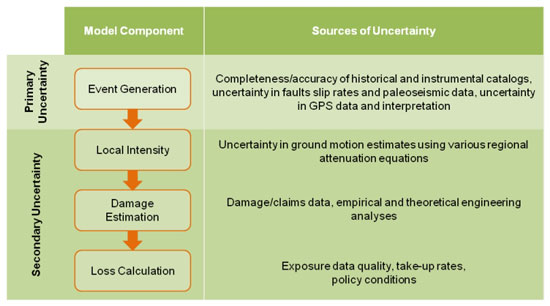
Ground motion calculations, which are the main constituent of the local intensity component of the model, provide the key inputs for damage estimation. Uncertainties in ground motion are propagated downstream through the loss estimation process, and the effect can be especially complex due to the nonlinear relationship between buildings response and the intensity of ground motions to which they are subjected. Thus, it is important to use the most robust and reliable ground motion prediction equations available.

How do models estimate ground motion at a particular site? When a fault ruptures during an earthquake, seismic waves radiate and propagate through the earth, passing through rocks with different material properties that reflect, refract, and scatter the waves. The intensity of these waves generally diminishes as they propagate away from the source. However, the nature of the large scale regional geological settings, basin effects, and local site conditions can create complexities that defy this general pattern.

Engineering seismologists derive empirical ground motion prediction equations (also called attenuation equations) in terms of measurable physical parameters of the earthquake source—such as magnitude—that are important in the generation of ground motion. They begin by formulating physical models that in their view best represent the relationships between the parameters of the causative fault rupture and the ground motion generated. Next, they collect, clean, and organize data from various earthquakes to create a database of source parameters and actual ground motion observations. Using statistical methods, they estimate values of the coefficients of the equation to minimize the ground motion prediction error. While assembling the prediction equations, focused effort goes into separating the effects of the source parameters, such as magnitude and faulting mechanism, from the path-related parameters, such as distance and rate of ground motion decay with distance.

For a given set of source and site parameters, the median ground motion from any such attenuation equation represents the best estimate of the "true" (but unknown) median of the ground motions generated by future earthquakes of the same source and site characteristics. However, as will be discussed in greater detail later, there are often significant variations in the median ground motion calculated using different equations.

The previous generation of attenuation equations, mostly developed in the 1990s, performed reasonably well in predicting ground motion for moderate magnitude and average distance combinations for which there is ample data. However, for relatively infrequent large-magnitude earthquakes, ground motion recordings, particularly at sites close to the faults, were historically scarce. The ground motion predictions in these instances were highly unreliable because the lack of data imposed a significant statistical limitation on the formulation of the attenuation equation in this large magnitude/short distance range. Because they were usually formulated based on judgment corroborated by a small set of recordings, they often diverged significantly from scientist to scientist, reflecting the differences in opinion of the researchers.

The Next Generation

In 2003, recognizing the shortcomings in relying on individual researchers to construct attenuation equations, the Pacific Earthquake Engineering Research Center (PEER) partnered with the USGS and the Southern California Earthquake Center to coordinate a large scale multidisciplinary project called the Next Generation Attenuation Models (NGA). The goal was to compile a global ground motion database from which to develop a set of robust attenuation equations for shallow crustal earthquakes, such as those that occur in the western U.S.

To create the database (the largest to date with more than 3500 recordings from approximately 170 events), the researchers applied a uniform data processing scheme for all ground motion recordings. The database includes such characteristics as source geometry, fault mechanism, source-to-site distances, and site conditions, all revisited, corrected, and compiled in a consistent manner and more accurately defined than ever before.

Five groups of researchers were given guidelines on the use of ground motion parameters, but were free to formulate the attenuation equations as they saw fit. The groups worked on the equations independently, but interacted frequently with each other, as well as with other experts, to discuss ideas and debate concepts. Because of the vastly superior quantity and quality of ground motion data, the NGA project resulted in a set of attenuation equations that are more robust and objective (data-driven) than any previously produced. Notably, all researchers found that ground motion from large magnitude earthquakes at close distances to be significantly lower than had been calculated by previous attenuation equations.

By starting with the same set of high quality ground motions (and thus reducing the potential bias imposed by the data), each NGA equation provides more realistic estimates of ground motion, which reduced uncertainty on the estimated median values compared with previous equations. Still, each NGA formulation remains unique, reflecting the author's view of the dependency of the ground motion on various source and site parameters. And even with a superior data set, there is still not enough data to fully constrain the models, resulting in different calculations of median ground motion (a follow-up project, NGA West II, is currently under way to resolve some of these issues and is due to be completed in 2012).

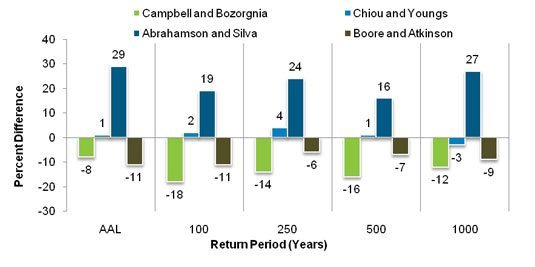
Although the NGA equations represent the current state of the art, the selection of which equation or equations to use can have a considerable impact on ground motion calculations (see the sensitivity analysis below). This translates into epistemic uncertainty (stemming from lack of knowledge), which needs to be properly understood and captured in catastrophe models for the results to be meaningful.

Understanding the Variability

The main source of uncertainty in attenuation equations stem from incomplete knowledge about the generation and propagation of seismic waves, and lack of data to formulate the process precisely. The complex physical phenomenon depends on myriad factors—including the exact mechanism of the earthquake rupture, and detailed seismic and geologic information about the interior of the Earth—that are not easily modeled using empirical or physical models. In fact, even if the process of ground motion generation at a site is completely understood and all the intricacies could be fully formulated, we still cannot perfectly predict ground motion because there is still considerably uncertainty in the input data used for ground motion prediction.

Consequently, there is always a residual that is the difference between the measured ground motion and the value predicted by the model at a given site. The choice of parameterization used by each NGA research group, based on their way of interpreting the data and regression techniques, determines the formulation of the residual.

The basic structure of a ground motion prediction equation is generally as follows:

GM = f(Source, D, Path, Site) + ε

where:

GM is the log of the ground motion, which is typically expressed in terms of spectral acceleration or peak ground acceleration

Source represents the parameters related to the earthquake source (such as magnitude, focal depth, faulting mechanism)

D is a measure of the distance from the rupture

Path represents the propagation path, including possible basin effects Site represents the local site effects

ε is the total randomness residual with respect to the median ground motion, which often is divided into the inter- and intra-event components²

In the NGA equations, the residual is formulated to be a normally distributed random term with a mean of zero and a standard deviation that represents the scale of the aleatory uncertainty. Put more simply, the NGA equation without the residual represents the median ground motion expected given a set of input variables, and the residual represents the variability around this median.

Capturing the Uncertainty

By the time the 2008 USGS national seismic hazard maps were published, four of the five NGA developers had published their research. Three of these—Boore and Atkinson (2008), Campbell and Bozorgnia (2008), and Chiou and Youngs (2008)—were incorporated into the new maps. The fourth group, Idriss (2007), produced a simplified attenuation equation with limited applicability, so it was not included in the USGS maps or in AIR's model. The fifth and final NGA equation—that of Abrahamson and Silva (2008)—was published after the USGS maps were published but was included in the AIR model.

With the exception of the Idriss equation, the equations developed by the NGA groups underwent extensive peer review and are equally valid. The differences in the median ground motions predicted by these empirical equations—which are magnified for large magnitude/short distance ranges that are still relatively poorly represented by the available data—reflect the epistemic uncertainty relative to the true median ground motion.

To capture this uncertainty, it is a common practice to combine models using a logic tree approach to take into account several independent expert opinions. The USGS's recommendation was to implement the attenuation equations with equal weight. AIR followed the USGS's recommendation in the AIR Earthquake Model for the United States, albeit with four equations rather than the three implemented by the USGS.

Sensitivity of Regional Loss to Choice of NGA Equation

AIR conducted a sensitivity study of the impact of the various NGA equations on industry losses. The chart below shows the percentage difference between California industry insured losses (residential, commercial, and auto) using a single NGA equation and using the combination of all four, equally weighted, as implemented in the AIR model. For example, using only the equation developed by Abrahamson and Silva, as opposed to the weighted average of all four, would increase modeled average annual losses by 29 percent. Thus losses are highly sensitive to the choice of attenuation equation(s), even though the four NGA equations are equally valid statistical representations of ground motion.

It is important to recognize that the choice of attenuation equations for ground motion analysis and the calibration of the vulnerability components of the model are closely linked. In theory, the vulnerability of buildings should be independent of the modeling of ground motion. However, because there is an insufficient number of recordings of actual ground motions, damage functions are calibrated based on a combination of recordings and simulated ground motion for locations for which there is no data. Thus, the choice of attenuation equations determines the simulated ground motion, which affects the calibration of damage functions to actual loss data. Consequently, the scale of loss variation shown in the sensitivity analysis above would likely be smaller were separate damage functions calibrated to each of the individual NGA equations separately.

Conclusion

Since the 2008 USGS National Seismic Hazard Maps were published, questions have arisen regarding the weights assigned to the attenuation equations and whether they might be appropriately changed in the AIR Earthquake Model for the United States Model. Yet, as was just noted, all attenuation equations used in the AIR model (and in the USGS maps) are statistically valid representations of earthquake ground motions.

While it is common to find that one attenuation equation provides a better fit for a particular set of earthquake data, such an observation is not statistically significant given both the statistical nature of attenuation equations and the considerable uncertainty in the earthquake process. Of course, it is entirely acceptable to have a different view from the USGS with respect to the weights. However, such a decision should be based on strong scientific reasoning, a thorough technical evaluation of the equations, and must be supported by data.

By supporting the development of multiple ground motion equations, the leading research institutions that sponsored the NGA project created a robust, objective, and scientifically defensible characterization of epistemic uncertainty in ground motion prediction. The scientific consensus is to weight the four NGA equations equally. It is an approach that takes epistemic uncertainty into consideration and thus—in the context of a catastrophe model—it is an approach that produces a more sound estimate of the expected loss.