Modeling Fundamentals: Understanding Uncertainty
Apr 18, 2018
Editor's Note: In this article, Dr. Jayanta Guin, AIR Chief Research Officer, introduces some key concepts and answers the fundamental questions: What is uncertainty, where does it come from, and how is it treated in models?
Since catastrophe models were first introduced in the late 1980s, the increase in computing power by several orders of magnitude and the relentless pace of scientific research have made possible dramatically more sophisticated simulation processes. The growth in detail and complexity of the models, as well as in the sheer number of parameters, may give the sense that models should be more precise than ever. While catastrophe risk management has undoubtedly come a long way, translating model results into informed decision-making requires a balanced understanding of uncertainty in model assumptions and parameters, and a judicious awareness of the limitations of modeling.
What Is Uncertainty?
Real world systems are immensely complex, and models that attempt to simulate them are essentially simplified mathematical representations of physical phenomena. This process of simplification introduces both possibilities and pitfalls. Probabilistic catastrophe models use science and statistics to make sense of seemingly random and unpredictable events in nature, allowing us to essentially prepare for the unknowable. On the other hand, how do we know if our models properly describe the physical world? How good are the data used to develop the models and the data input into the models? Have we simplified too much?
All these concerns fall under the notion of uncertainty, which at a conceptual level can be categorized into two broad types—epistemic (from the Latin root episteme, or knowledge) and aleatory (from the Latin root alea, a game of dice). Epistemic uncertainty results from an incomplete or inaccurate scientific understanding of the underlying process and lack of data on the process to make statistically unbiased estimates of future outcomes. In theory, as we understand the process better and more data becomes available, the size of epistemic uncertainty diminishes. Aleatory uncertainty, on the other hand, is attributed to intrinsic randomness and is not reducible as more data is collected. In practice, the distinction between these two types of uncertainty is not always clear, as there are situations where apparent randomness is actually a result of lack of knowledge.
Whatever its source, uncertainty ultimately imposes limitations on the accuracy of the model’s output. Uncertainty is not confined to final modeling results, however; it is present in each component of the modeling framework, both in models and in model parameters (see table below).
Dr. Jayanta Guin, Ph.D.
Chief Research Officer
Edited by Nan Ma, CEEM
The article:
• Understanding uncertainty in model assumptions and parameters is essential in translating model results into informed decision-making
• Uncertainty is present in both the event generation component of the model (primary uncertainty) and in the damage and loss calculation components (secondary uncertainty)
• Epistemic uncertainty results from imperfect knowledge, while aleatory uncertainty results from randomness
| Model | Parametric | |
|---|---|---|
| Epistemic | Whether the model appropriately represents the physical phenomenon. This type of uncertainty can be accounted for by considering alternate models, or using the weighted average of several models. | Uncertainty regarding the distribution of possible parameter values. Sources include data quality and data completeness, so it is reduced as more data becomes available. |
| Aleatory | The misfit between the model predictions and the actual observations (unexplained variability). Can contain an epistemic component because it considers the effects of missing variables or variables intentionally left out of the model. | The irreducible randomness in the estimation of the model parameters. It is an understood variability and is propagated through the model. |
How Is Uncertainty Addressed in Catastrophe Models?
In discussing uncertainty, different disciplines prefer different terminology. Scientists apply the terms epistemic and aleatory uncertainty to their understanding of physics-based phenomena. Actuaries and statisticians, who deal with the frequency and severity of potential events, tend to prefer the terms model and parametric uncertainty.
To better conceptualize uncertainty in catastrophe models, which combine complex probabilistic and physical submodels with statistical and actuarial science, it is necessary to introduce yet two more terms—primary and secondary uncertainty. Primary uncertainty refers to uncertainty in the event generation component of the model—in other words, in the event catalog. Secondary uncertainty is uncertainty in the damage estimation. Both types have elements of epistemic/aleatory as well as model/parametric uncertainty.
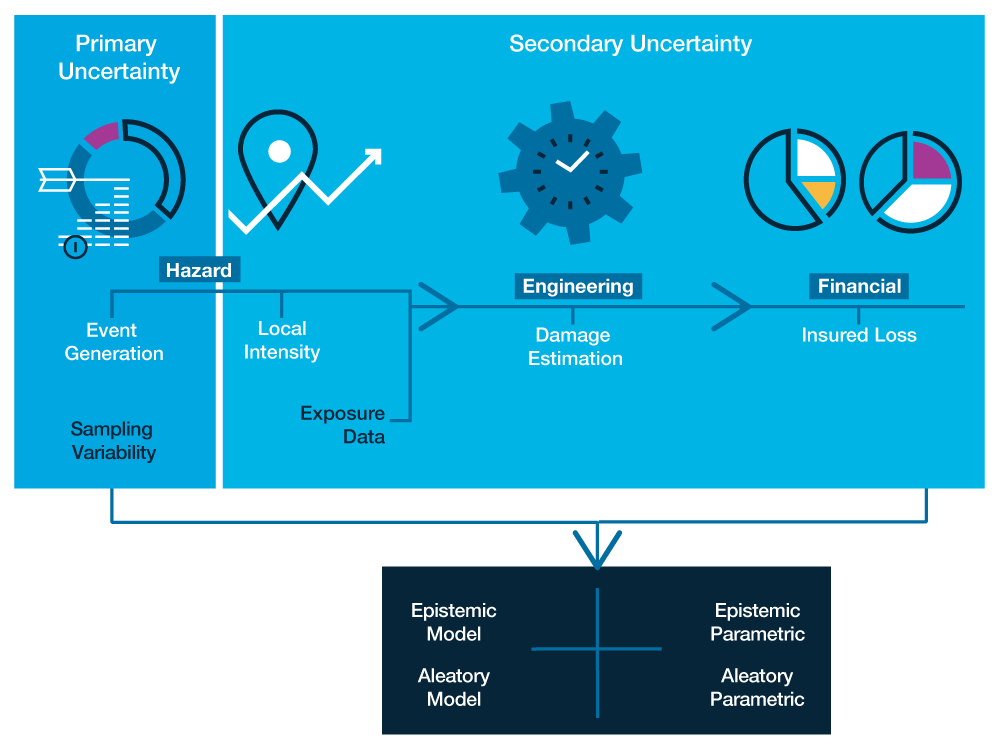
Primary Uncertainty
In constructing an event catalog that reliably reflects the potential risk from future events, the main sources of epistemic uncertainty are data quality, data completeness, and incomplete scientific understanding of the natural phenomenon being modeled. The historical record for events that predate modern instrumentation is considerably less reliable, and smaller intensity events are more likely to have gone unrecorded. Furthermore, large intensity events are rare, so relying on the historical record can misrepresent the tail risk from low frequency but high impact events.
To address this uncertainty, AIR scientists and statisticians construct stochastic event catalogs by fitting probability distributions to the historical data for each event parameter (for example, magnitude of an earthquake or minimum central pressure of a cyclone). Due diligence requires reviewing, processing, and validating data from multiple sources. In addition, where available, geophysical information (such as GPS observations or fault trenching data) is used to supplement historical data.
Using the same set of observable data—but different underlying assumptions for processes that are not directly measurable (such as the time dependency of fault rupture probability, or the link between warm sea surface temperatures and increased hurricane landfall frequencies)—alternate credible views of risk may be possible. AIR offers multiple stochastic catalogs for certain models, such as standard and climate-conditioned catalogs for the U.S. hurricane model, and time-dependent and time-independent earthquake catalogs for the U.S. and Japan. In the absence of a clear consensus in the scientific community, a multiple-catalog approach better captures the most current state of knowledge.
The process of creating event catalogs suitable for practical computational platforms introduces another type of primary uncertainty, called sampling variability, which is associated with catalog size. A catalog with more scenario years (100,000) has inherently less sampling variability than a smaller catalog (50,000 or 10,000 years) because it better reflects the full range of possible outcomes for the upcoming year. While this source of variability can in theory be eliminated by drawing ever larger samples of events, for the purposes of computational efficiency and workflow requirements (a larger catalog translates to longer analyses times), it is desirable to statistically constrain the catalog. AIR uses various techniques to sample a smaller set of events that provide a reasonable approximation of the results obtained using a larger set.
Secondary Uncertainty
Secondary uncertainty is the uncertainty associated with the damage and loss estimation should a given event occur. Part of this can be attributed to uncertainty in the local intensity (ground motion or wind speed) of a particular event at a given location. The ground motion prediction equations used in earthquake models and the wind field profiles used in hurricane models are physical and statistical representations of very complex phenomena. Depending on the underlying assumptions, parameters, and the set of data used, different equations (i.e., alternative models) for calculating local intensity are possible, and the choice of which model or models to use constitutes epistemic model uncertainty.
Translating local intensity to building performance is another source of secondary uncertainty. Because actual damage data is scarce, especially for the most severe events, statistical techniques alone are inadequate for estimating building performance. As a result, AIR constructs damage functions based on a combination of historical data, engineering analyses (both theoretical and empirical), claims data, post-disaster surveys, and information on the evolution of building codes. While graphical representations of damage functions typically only show the mean damage ratio, there is actually a full probability surface that allows for non-zero probabilities of 0% or 100% damage. This probability surface encapsulates the aleatory uncertainty in the estimation of both the local intensity and damage.
This brings us to a final point about uncertainty in damage estimation, and ultimately, in insured losses. As past catastrophes have demonstrated, the reliability of model output is only as good as the quality of the input exposure data. Uncertainties or inaccuracies in building characteristics or replacement values can propagate dramatically into the estimates of losses.
Improving the Quantification of Uncertainty—Recent Research
Not only is our understanding of catastrophes continuously improving, but so is our ability to characterize uncertainty in our models. One example is the seismicity formulation for the New Madrid Seismic Zone in the central United States. Unlike our notional example of a fault that breaks every 10 years on average, real-world earthquake rupture is far more complex and is driven by factors that we don’t yet fully understand. In 1811-1812, a series of three violent earthquakes occurred in this region, near the borders of Arkansas, Illinois, Indiana, Kentucky, Missouri, Ohio, and Tennessee.
The exact magnitudes of events are not known, nor the precise location of the causative fault or the recurrence interval. As scientists have learned more about the NMSZ throughout the years, the seismicity formulation has evolved to become more complex to account for the uncertainty in parameters and possible alternative models. Seismologists have adopted a logic tree approach to represent the possible alternative models or parameters, with each branch weighted according to its assessed probability of occurrence.
The latest view from the USGS published in 2014, which was extensively reviewed by AIR and incorporated into the AIR Earthquake Model for the United States, includes five hypothetical fault traces to account for the spatial uncertainty of future earthquakes in this region, a range of rupture magnitudes for each fault segment, a distribution of recurrence intervals, and multiple cluster rupture scenarios. The resulting possible permutations, illustrated in the logic tree in Figure 3, is incorporated into our optimized stochastic catalogs and captures all known sources of uncertainty regarding earthquake rupture in this seismic zone.
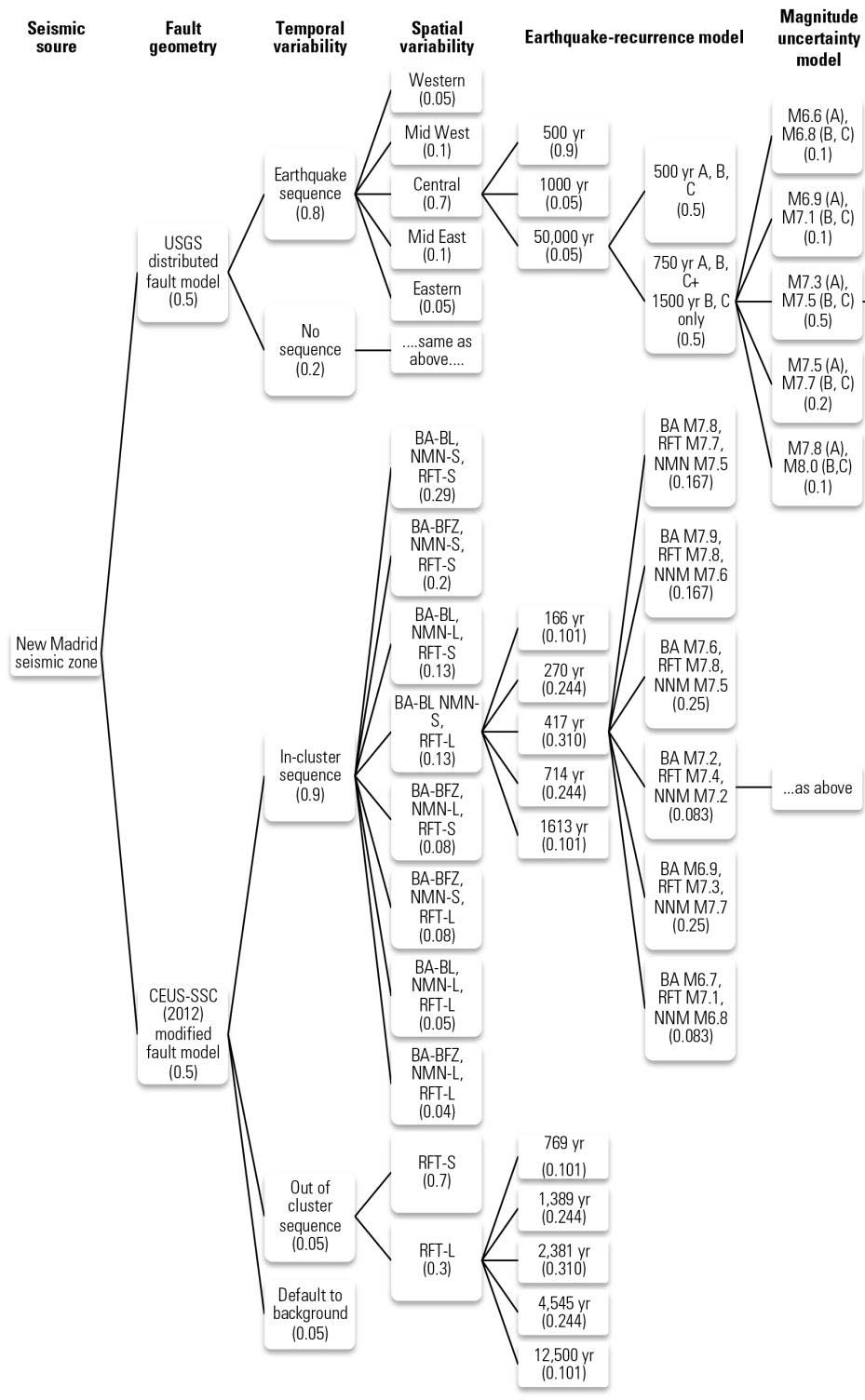
Therefore, while our models provide a single view of risk, this view encapsulates alternative theories and knowledge from many experts. While we’ve heard some model users express that they would like to see multiple views of risk, decisions that are informed by model output are deterministic in nature—for example, a price for a home insurance premium or reinsurance contract.
Model users should not assume that more choice is necessarily a suitable approach to addressing uncertainty. This is all the more important to recognize because risk is very sensitive to changes in the underlying estimates of hazard. Our many decades of model development experience at AIR have shown that seemingly independent and well validated model components do not guarantee a robust model when pieced together. AIR’s development process does not merely entail a selection of subcomponents, but requires a deep and comprehensive understanding of the overall model and its ultimate goal: to produce realistic and reliable estimates of loss. AIR will continue to explore the possibility of offering multiple views of risk, as long as the additional flexibility provides clear value to our model users.
Conclusion
Every model update attempts to reduce uncertainty by incorporating cutting-edge research and the latest available observations and claims data. AIR’s methodology is transparent, rigorous, and scientifically defensible. Our researchers undertake a meticulous review of scientific literature and conduct their own research where appropriate. Uncertainty is carefully considered and incorporated in the model components, each of which is thoroughly calibrated and validated against actual data.
To be sure, there is still much to be improved upon. The future of catastrophe modeling lies in further advancing the state of scientific knowledge and in refining how uncertainty is addressed and reported. However, even with a perfect understanding of the physical world (which we are far from claiming), there will still be pure—and irreducible—randomness in nature. Uncertainty is an inherent part of catastrophe models. But lacking a firm sense of where it comes from and how it is addressed in the models, the most skeptical may dismiss the value of catastrophe modeling and consider it futile in the face of so much uncertainty. Without uncertainty, however, there would be no risk, and without risk, no insurance.
For model users to effectively mitigate losses and to identify business opportunities, it is important to be able to recognize and understand uncertainty—both inherent in the model and introduced by input exposure data—and to incorporate the most comprehensive and robust view of risk into their decision-making processes.
