A Martian’s View of Hurricane Climatology: An Allegory for Bayesian Learning

Over the course of several more years of productive scientific study, you meet a nice Earthling, get married, and decide to settle down and make Earth your home. You continue to monitor tropical cyclone activity over the course of a long and fruitful scientific career. After many decades have passed, you send the following update to your Martian colleagues:

One of the most interesting features of hurricane activity I have witnessed firsthand over the years has been the impact of large-scale variations in climate. During El Niño events, which occur roughly every 2-7 years, tropical cyclone activity is enhanced in the Pacific Ocean, but suppressed in the Atlantic. Low frequency, multidecadal changes in underlying sea surface temperatures in each basin also modulate the number of cyclones that form each year. And in the North Atlantic Ocean Basin, hurricane paths are influenced by the position of a pressure high whose location varies as part of a phenomenon called the North Atlantic Oscillation. Since the storms tend to take the path of least resistance around the high, changes in its position influence which stretches of coastline are at greatest risk for TC landfalls.

The high winds of landfalling cyclones can cause severe damage to Earthling homes, which is why we just bought waterfront property in Makkovik, a small town in the Labrador region of Canada. My Earthling better-half and I plan to spend our retirement enjoying the ocean here, where I have never observed a landfalling cyclone and I estimate the lowest possible likelihood of landfalls.

The way the Martian physicist constructed a mental model about hurricane climatology over many years of observation mirrors the practice of modeling to make Bayesian inference. Before the consideration of any data in Bayesian statistics, the modeler first develops a prior model for the process of interest. The prior model is an aptly named probabilistic description of the modeler's prior beliefs about the process before any data have been observed. It may be informed by scientific expertise—for example, the Martian physicist knew from an understanding of fluid dynamics and the directional spin of the Earth that Earthling winds would tend to carry cyclones from east to west if they formed in the tropics, and knew from thermodynamic considerations that warm sea surface temperatures would be needed for such storms to form. Beyond these types of broad-brush descriptions, however, the prior model is intended to be as vague as possible.

The object of the analysis is to use observations about the phenomenon under study to "update" the prior model and sharpen its vague assignment of probabilities. To decide how much influence to give the data in the final estimate, the modeler must construct a data model that quantifies the uncertainty of the observations. When using the data to make inferences, a data model that characterizes observations as very uncertain will have a lesser impact in updating the prior model than a data model that characterizes the observations as having a clear signal with little uncertainty (as in the comparative results in the left and right panels of Figure 1). For our Martian physicist, the conclusions drawn from the observations made with the damaged Cycloscope v3000 will be slightly more uncertain than if the instrument had made the trip to Earth without sustaining any impairment. In fact, highly accurate data can completely eclipse the information in the prior model if it is inconsistent with the observation.

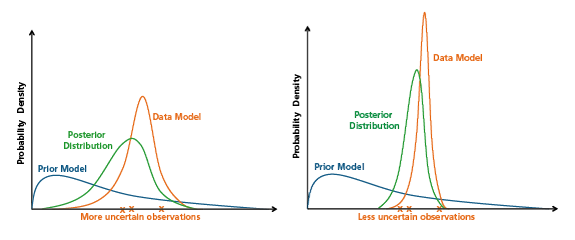
The probabilistic estimate of the process that emerges from a Bayesian analysis when the prior model, data model, and data themselves are combined is called the posterior distribution. The fact that the Bayesian "answer" to scientific questions is a full probability distribution is one of the distinctive hallmarks of this approach, and one that enables rich, multifaceted analysis.

For example, if the Martian physicist derives a posterior probability distribution for the locations, sea surface temperatures, and environmental wind conditions under which tropical cyclones tend to form, the distribution can be queried to figure out, for example, the probability of tropical cyclones forming below any specific temperature, whether that probability varies by region, and how that probability changes as a function of local winds.

Bayesian approaches are becoming increasingly popular tools for modeling geophysical systems (Berliner, 2003; Tebaldi et al., 2004; Elsner and Jagger, 2013). The paradigm boasts three major draws.

First, the process of formulating a Bayesian model is based on intuitive specification of relationships between variables that reflects the way scientists already think about their subject matters. Developing the prior model is akin to establishing a background understanding based on existing facts and theory before collecting data in the field. Meanwhile, constructing a data-level model is analogous to understanding the mechanics, reliability, and precision of the instrumentation used to collect data.

The second reason for the burgeoning popularity of the Bayesian approach is an increasing recognition that complex problems with multiple sources of uncertainty deserve probabilistic answers that account for that uncertainty. Because model development gets broken into conditional modules in the Bayesian paradigm, the uncertainty can be described separately for each component part of the model. The parts are then combined using the formal laws of probability to get a fully probabilistic answer.

The third enticing attribute is the ease with which scientific knowledge can be integrated into Bayesian models. Such information can be incorporated through probability distributions carefully designed to reflect expert understanding of the systems at hand, or more explicitly, through direct use of state-of-the-art mechanistic models developed by domain-area scientists.

Although developed in the 1700s and 1800s—much earlier than the more commonly known body of frequentist statistical methods—Bayesian data analysis did not gain much momentum until the advent of modern computing in the 1980s. In most real-world problems of any complexity, Bayesian inference depends on drawing large samples from the posterior probability distribution, which can still require quite a bit of processing time.

However, with ever-faster, ever-cheaper computers, as well as continuing development of smarter algorithms by the research community, it is now feasible to exploit the strengths of this method to solve even relatively complex, high-dimensional problems of great interest, like those present in catastrophe modeling. In the second article of this two-part series, we will discuss results from just such a Bayesian model of the frequency and spatial distribution of landfalling tropical cyclones in the North Atlantic basin.